We’re working on a new project in FYS4460 about percolation. In the introduction of this project, we are given a few commands to help us demonstrate a few properties of percolation clusters using MATLAB.

As the Python-fan I am, I of course had to see if I could find equivalent commands in Python, and thankfully that was quite easy. Below I will summarize the commands that will generate a random matrix of filled and unfilled areas, label each cluster in this matrix and calculate the area of each such cluster. Finally, we’ll draw a bounding box around the largest cluster.

First of all, we need to include the pylab package together with the scipy.ndimage.measurements package:

from pylab import *
from scipy.ndimage import measurements

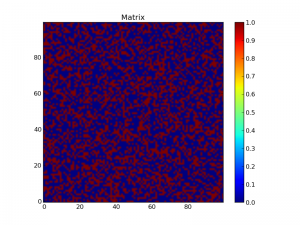
Now, let’s create a random matrix of filled and unfilled regions and visualize it:

L = 100
r = rand(L,L)
p = 0.4
z = r < p

imshow(z, origin='lower', interpolation='nearest')
colorbar()
title("Matrix")
show()

This creates a matrix of random numbers r before creating a map z of this matrix where each element is set to True if r < p and False if r > p:

Visualization of the map z. Visualization of the map z.

Furthermore we want to label each cluster. This is performed by the scipy.ndimage.measurements.label function:

lw, num = measurements.label(z)
imshow(lw, origin='lower', interpolation='nearest')
colorbar()
title("Labeled clusters")
show()

This labels each cluster with a number which may be visualized using the imshow function as above:

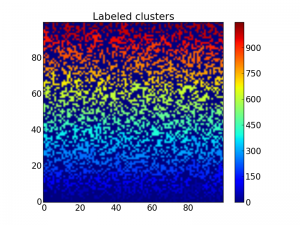Matrix with labeled clusters, so it is a bit hard to distinguish each cluster. Matrix with labeled clusters, so it is a bit hard to distinguish each cluster.

Beacause the label starts from the bottom up, the cluster colors are a bit too ordered, making it hard to distinguish two clusters close to each other. To fix this, we may shuffle the labeling with the following code:

b = arange(lw.max() + 1)
shuffle(b)
shuffledLw = b[lw]
imshow(shuffledLw, origin='lower', interpolation='nearest')
colorbar()
title("Labeled clusters")
show()

Now it is way easier to see the different clusters:

The same matrix with all clusters labeled with a number. The same matrix with all clusters labeled with a number.

After this we may want to extract some properties of the clusters, such as the area. This is possible using the scipy.ndimage.measurements.sum function:

area = measurements.sum(z, lw, index=arange(lw.max() + 1))
areaImg = area[lw]
im3 = imshow(areaImg, origin='lower', interpolation='nearest')
colorbar()
title("Clusters by area")
show()

The above code now plots the same matrix as above, but this time with all clusters colored by area:

Matrix with the clusters colored by area. Matrix with the clusters colored by area.

Finally, we may want to find the bounding box of the largest cluster, so we again may see if there is a path from one side to the other. This is possible by using the function scipy.ndimage.measurements.find_objects. Note however that this is a bit risky. If there are two clusters that are largest with the same area, find_objects will find the bounding box of both clusters. I’ll leave it up to you to figure out a method to avoid this if necessary. (Pro tip: Make a mapping of the cluster labels to the areas.)

With the find_objects function, we are able to plot a rectangle around the largest cluster:

sliced = measurements.find_objects(areaImg == areaImg.max())
if(len(sliced) > 0):
    sliceX = sliced[0][1]
    sliceY = sliced[0][0]
    plotxlim=im3.axes.get_xlim()
    plotylim=im3.axes.get_ylim()
    plot([sliceX.start, sliceX.start, sliceX.stop, sliceX.stop, sliceX.start],
                     [sliceY.start, sliceY.stop, sliceY.stop, sliceY.start, sliceY.start],
                     color="red")
    xlim(plotxlim)
    ylim(plotylim)

show()

This shows up like this:

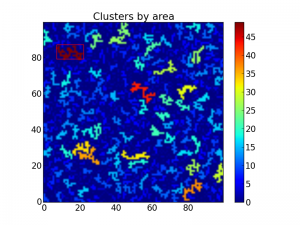bounding-box A bounding box on top of the largest cluster. The rest are colored by area.

The whole program then becomes as follows:

from pylab import *
from scipy.ndimage import measurements

L = 100
r = rand(L,L)
p = 0.4
z = r<p

figure(figsize=(16,5))
subplot(1,3,1)
imshow(z, origin='lower', interpolation='nearest')
colorbar()
title("Matrix")

# Show image of labeled clusters (shuffled)
lw, num = measurements.label(z)
subplot(1,3,2)
b = arange(lw.max() + 1) # create an array of values from 0 to lw.max() + 1
shuffle(b) # shuffle this array
shuffledLw = b[lw] # replace all values with values from b
imshow(shuffledLw, origin='lower', interpolation='nearest') # show image clusters as labeled by a shuffled lw
colorbar()
title("Labeled clusters")

# Calculate areas
subplot(1,3,3)
area = measurements.sum(z, lw, index=arange(lw.max() + 1))
areaImg = area[lw]
im3 = imshow(areaImg, origin='lower', interpolation='nearest')
colorbar()
title("Clusters by area")

# Bounding box
sliced = measurements.find_objects(areaImg == areaImg.max())
if(len(sliced) > 0):
    sliceX = sliced[0][1]
    sliceY = sliced[0][0]
    plotxlim=im3.axes.get_xlim()
    plotylim=im3.axes.get_ylim()
    plot([sliceX.start, sliceX.start, sliceX.stop, sliceX.stop, sliceX.start],
                     [sliceY.start, sliceY.stop, sliceY.stop, sliceY.start, sliceY.start],
                     color="red")
    xlim(plotxlim)
    ylim(plotylim)

show()